When Factoring How Do You Know Wherer to Put the -

Factoring Quadratics: The Simple Case

A "quadratic" is a polynomial that looks like "a10 ^two + bx + c", where "a", "b", and "c" are only numbers (and either of b and c, merely never a, might be zero).

For the like shooting fish in a barrel case of factoring quadratic polynomials, nosotros volition need to find two numbers that will multiply to be equal the constant term c, and volition as well add together upwards to equal b, the coefficient on the linear x -term in the center. Why?

Quadratics are degree-two polynomials. When you were learning how to multiply polynomials together, they probably started you out by multiplying ii binomials together (and they probably referred to this process as "FOILing").

Content Continues Beneath

To end up with a quadratic that had a leading coefficient of 1 (and no fractions), each of the original binomials besides had to take had a leading coefficient of 1.

Looking at two generic binomials (using the variable x and the generic numbers p and q), we can multiply the binomials like this:

(x + p)(x + q)

x ^two + p10 + q10 + pq

10 ² + (p + q)x + pq

In the above, (p + q) = b and pq = c from " ten ² + bx + c". This multiplication and simplification explains why, to factor a quadratic, we'll need to start by finding the 2 numbers (being the p and the q above) that add up to equal b, where those numbers also multiply to equal c. It's required by the logic of factoring (and factoring the quadratic is the "undo" of the original binomial multiplication).

(By the style, I call this topic "factoring quadratics", where your textbook may refer to this topic as "factoring trinomials". But a "trinomial" is any iii-term polynomial, which may not be a quadratic (that is, a degree-2) polynomial. And not all quadratics have 3 terms. And then the book's section or chapter title is, at best, a fleck astray. Don't worry near the deviation, though; the volume's championship means the same thing every bit what this lesson explains.)

Here'due south what the "elementary" quadratic-factorization process looks like, in practice:

• Gene x ⁱⁱ + 5ten + half-dozen

This quadratic has a leading coefficien of one, so this is the simple instance of factoring. To get started, I need to find factors of c = +6 that add together upward to b = +5. I take two options, because vi factors as the product of 2 and 3, or equally the product of 1 and 6.

Now, because I'thousand multiplying to a positive 6, so my factors accept to have the same sign; they must both be positive or else they must both be negative, because that's how negatives piece of work. Considering I'yard adding to a positive 5, and so both factors must be positive.

I'll check the sums of the pairs of potential factors, to see which works:

Since I need my factors to sum to plus-five, then I'll be using the factors +two and +three.

From back when I learned how to multiply polynomials, I know that they got this quadratic by multiplying two binomials. Because the leading coefficient is only 1, I know that the leading coefficient of each of those binomials must also have been just 1. This means that the production started out looking something like this:

(x     )(x     )

At the ends of each parenthetical go the numbers that multiply to +6 and add to +five. This means that I can stop my factoring past plugging those numbers into my parentheticals, in either order:

(x + 2)(ten + 3)

Why "in either order"? Considering the front ends of the two parentheticals were the same, so I'd take ended up with the same factorization, either way. Remember: order doesn't affair in multiplication.

---

This is how all of the "like shooting fish in a barrel" quadratics will piece of work: nosotros find factors of the constant term that add up to the middle term, and so nosotros use these factors to fill in our parentheses.

By the mode, we can always bank check our piece of work by multiplying our factors back together, and bank check that we have gotten dorsum to the original answer. To cheque the to a higher place factorization, the multiplication goes like this:

---

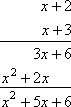
Your text or instructor may refer to factoring "by grouping", which is covered in the lesson on simple factoring. In the "easy" case of factoring, using the "grouping" method simply gives yous some actress piece of work. For example, in the to a higher place problem, in add-on to finding the factors of +6 that add to +5, you would have had to practice these additional steps:

x ² + 5x + 6

x ² + 3ten + twoten + 6

(x ² + threex) + (2ten + six)

ten(x + 3) + 2(ten + 3)

(x + 3)(x + 2)

You would get the same answer as I did, but (I retrieve) it'south easier to just get straight to filling in the parentheses.

---

• Gene x ² + 7x + 6

The leading term is merely i, so this is the simple case of factoring. The constant term is half-dozen, which tin be written equally the production of 2 and 3 or of 1 and half-dozen, just as in the previous practice. Simply the coefficient on the centre term is different this time. Instead of a +five, I've got a +7.

The sign on the constant term is the same as before (namely, a "plus"), so I'll still need to "plus" factors. But the sum (that is, the centre-term'south coefficient) is unlike; information technology's now a 7. Whereas 2 + 3 = 5 worked for the previous quadratic, +2 and +3 are not the numbers I need in this case. On the other hand, ane + half-dozen = +7, so I'll use +i and +six for my factorization. And I'll besides go directly from having fatigued this conclusion to writing down my last answer:

(x + i)(ten + 6)

Again, think that the order doesn't matter in multiplication, so the to a higher place respond could every bit-correctly exist written every bit "(x + six)​(x + 1)".

---

• Factor x ^two – vten + vi

The constant term (created by multiplication) is +6, so my factors will be either both "plus" or else both "minus". But the middle coefficient this time is "minus". Since I'1000 adding to a "minus", (namely, to –v), then both factors must exist "minus".

When the eye term's coefficient had been a "plus" v, I'd used factors +2 and +3. Now that my middle term's coefficient is "minus", I will use –ii and –3:

(x – 2)(ten – three)

---

Note that we can use clues from the signs to determine which pairs of factors to utilize, as I demonstrated in the previous exercises. The rules, formally, look similar this:

• If c is "plus", and so the factors will be either both "plus" or else both "minus".
• If b is "plus", so the factors are both "plus".
• If b is "minus", then the factors are both "minus".
• In either case, await for factors that add to b.

• If c is "minus", then the factors will be of alternating signs; that is, one will be "plus" and one will be "minus".
• If b is "plus", so the larger of the two factors is "plus".
• If b is "minus", then the larger of the two factors is "minus".
• In either case, look for factors that subtract to b; that is, factors which are b units apart.

---

• Cistron x ^two – 7ten + 6

The leading coeficient is 1, so this is a elementary-factoring quadratic. I am multiplying to a "plus" 6, so the factors volition be either both "plus" or else both "minus". Looking at the middle term, I see that I am adding to a "minus" vii, and then my factors will both be "minus".

The (negative) factors of +vi that add up to 7 are –1 and –6, so I will use –1 and –vi for my factorization:

(ten – one)(x – vi)

---

So far, c (the constant term) has always been a "plus". What if c is a "minus"?

• Factor x ⁱⁱ + x – six

Since I am multiplying to a "minus" 6, I need factors that have opposite signs; that is, one factor volition exist "plus" and the other will be "minus". The coefficient on the middle term is a "plus" 1, then I know that the larger of the two factors (larger, that is, in terms of its absolute value) volition get the "plus" sign. Since these opposite-signed numbers will be added together to get +one, then I need the 2 factors to be i unit of measurement apart.

The factor pairs for 6 are one and 6, and 2 and 3. The values in the 2nd pair are one unit apart, and so I know that I will be using 2 and iii.

Because I need to get a "plus" answer for the sum of the two factors, I'll need the larger of my two numbers to get the "plus" sign; namely, the 3 will be getting the "plus" sign (then the ii gets the "minus" sign). Then my factorization is:

(x – 2)(ten + 3)

---

• Factor x ⁱⁱ – x – six

This looks merely similar the previous quadratic, except that at present the middle term is "minus". The constant term is still "minus", so I still want factors with contrary signs. And the center term'southward coefficient (other than its sign) is however 1, and so I all the same want factors that are one unit of measurement apart. But this fourth dimension the larger cistron will get the "minus" sign.

All the other considerations remain the same. I still want factors of vi that are one unit autonomously, and so I'll still be using 2 and iii. Only this time, the sign on the 3 will be a "minus":

(x – three)(ten + 2)

---

• Cistron x ² – 5x – half-dozen

In this quadratic, the constant term is "minus", so I still want factors of contrary signs.

However, this time, the center term's coefficient (other than its sign) is 5 rather than ane, so now I want my two factors to exist five units apart. And considering the middle term's coefficient is "minus", the larger of my two factors volition become the "minus" sign.

The factor pairs for six are 1 and 6, and 2 and 3. The numbers in the first pair of factors are five apart, and so I'll be using the numbers 1 and 6. I'1000 calculation to a "minus", so I'll give the larger of my factors the "minus" sign; that is, I'll be using +1 and –6 for this factorization:

(x – six)(x + 1)

---

There is ane special case, by the way, for factoring quadratics. Back when you were factoring manifestly old numbers, there were some numbers that didn't factor, such equally five or 13. Recall that these unfactorable numbers are called "prime" numbers. You could always multiply two whole numbers to get another whole number, but some whole numbers could not be divided to get two (non-trivial) whole numbers.

Similarly, there are quadratics that won't gene. You can multiply 2 binomials (without fractions) to get a quadratic (without fractions), but not all quadratics tin exist factored to get ii (non-picayune) binomials. The terminology for such quadratics (or any un-factorable polynomial) is as well "prime".

• Gene x ^two + 710 – 6

The leading coefficient is one, and then this is a case of unproblematic factoring. Since the abiding term is "minus", I'll be needing a "plus" factor and a "minus" such that, when I multiply them together, I get –6, just when I add together them, I go +seven. In other words, I'll demand two factors that are seven units autonomously, with the larger factor getting the "plus" sign.

The cistron pairs for 6 are 1 and 6, and 2 and 3. At showtime glance, I may presume that I should utilise 1 and half dozen, but —

Ane of the factors has to exist "minus" in guild to multiply to get a "minus" six! Trying the first factor pair of ane and vi, the sum would be i of the following:

(–1) + 6 = 5

1 + (–6) = –5

Okay; neither way worked. And then perhaps I should be using the other factor pair...? Checking the add-on with those numbers, I become:

(–2) + 3 = i

2 + (–3) = –i

One might remember, "Well, maybe I should should exercise the signs differently." But the only way to get factors of six to add upward to vii is to give those factors the same sign. But if I do that, so the factors won't multiply to a "minus" vi.

In other words, there is no pair of factors of –6 that will add to +7. And if something isn't factorable, then it's prime. So x ² + 7x – 6 is a prime quadratic polynomial. In technical terms, it is "unfactorable over the integers", then-called because I couldn't detect a pair of integers that would piece of work. Then my answer is:

prime number

woodruffboun1945.blogspot.com

Source: https://www.purplemath.com/modules/factquad.htm

Bagikan Artikel ini